机器学习入门：2. 数据挖掘基础

1. 数据质量(Data Quality)

常见问题：

噪声：比如录音里面的环境噪音
异常：跟其他数据格格不入的数据，比如姚明的身高
缺失：数据没了
重复：数据重复

2. 相似度与距离(Similarity & Distance/Dissimilarity)

A. 相似度

两个数据有多相似，那么与之相对应的就有了不相似程度。

为什么这个重要，主要是观察周期性的，比如去年的太阳升起的时间跟今年的同一天就会很相似。

1. 余弦相似度 (Cosine Similarity)

\cos(\theta)=\frac{\mathbf{x}\cdot \mathbf{y}}{||\mathbf{x}|| \, ||\mathbf{y}||}

假设有两个人：

• 小王：喜欢 🎵 音乐、⚽ 足球、📚 阅读

• 小李：喜欢 🎵 音乐、⚽ 足球、📚 阅读、🎮 游戏

我们可以把他们的兴趣表示成一个“兴趣向量”：

• 小王 = (1, 1, 1, 0)

• 小李 = (1, 1, 1, 1)

（顺序分别表示：音乐、足球、阅读、游戏；1=喜欢，0=不喜欢）

⸻

1. 欧氏距离的结果

小王和小李的向量差是 (0,0,0,-1)，欧氏距离 = 1
好像差很多，但其实他们大部分兴趣是相同的。

⸻

2. 余弦相似度的结果

\cos(\theta)=\frac{(1,1,1,0)\cdot(1,1,1,1)}{||(1,1,1,0)|| \cdot ||(1,1,1,1)||}

分子 = 1×1 + 1×1 + 1×1 + 0×1 = 3
分母 = √(1²+1²+1²+0²) × √(1²+1²+1²+1²) = √3 × 2 = 3.46
相似度 = 3 / 3.46 ≈ 0.87

说明他们兴趣非常相似（角度夹得很小）。

2. Jaccard 系数 (Jaccard Similarity)

Jaccard 系数是 衡量两个集合相似度 的指标。

J(X,Y)=\frac{|X \cap Y|}{|X \cup Y|}

还是刚才的例子，

假设有两个人：

小王：喜欢 🎵 音乐、⚽ 足球、📚 阅读
小李：喜欢 🎵 音乐、⚽ 足球、📚 阅读、🎮 游戏

我们可以把他们的兴趣表示成一个“兴趣向量”：

小王 = (1, 1, 1, 0)
小李 = (1, 1, 1, 1)

（顺序分别表示：音乐、足球、阅读、游戏；1=喜欢，0=不喜欢）

Jaccard 系数的结果

交集（两人都喜欢的）= {音乐, 足球, 阅读} → 大小 = 3
并集（至少一人喜欢的）= {音乐, 足球, 阅读, 游戏} → 大小 = 4
Jaccard 系数:

J = \frac{|交集|}{|并集|} = \frac{3}{4} = 0.75

结果表明两人的兴趣相似度高达 75%，更符合直观。

3. 相关系数 (Correlation Coefficient)

相关系数（通常指 皮尔逊相关系数 Pearson’s r）衡量两个变量的 线性关系强度与方向。

皮尔逊相关系数（Pearson’s r）的定义是：

r = \frac{\text{Cov}(X,Y)}{\sigma_X \, \sigma_Y},r = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum (x_i - \bar{x})^2 \cdot \sum (y_i - \bar{y})^2}}

a. \text{Cov}(X,Y) = 协方差

协方差刻画了两个变量是否一起变动, 就是有没有关联。比如身高体重就有一定关联性。

\text{Cov}(X,Y) = \frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})

正相关就大于0，负相关小于0，无相关等于0。

b. \sigma_X、\sigma_Y = 标准差

这个是用来标准化的。比如身高体重的关联性。如果我突然把身高单位变成了 km，体重单位变成了 mg，那么上面的数值相较于cm，和 kg，就会有上亿倍的数值差距。那么这个数值你就看不懂了。

所以需要标准化一下，把这个单位给消除掉，就跟小时候做数学应用题有时候不加单位符号会有问题，但是我们如果加了标准化的处理，那么就能规避掉小时候的问题。这时候的数值真的就变成了一个绝对意义的数字。

而这个数字，也叫做 无量纲的值。（就是没有量词了）

\sigma_X = \sqrt{\frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^2}, \quad \sigma_Y = \sqrt{\frac{1}{n}\sum_{i=1}^n (y_i-\bar{y})^2}

c. 皮尔逊相关系数 Pearson’s r

r = \frac{\text{Cov}(X,Y)}{\sigma_X \, \sigma_Y}

因为标准差总是正数，所以 r 的取值一定在 [-1,1]。

当 X,Y 完全线性正相关时，协方差 = \sigma_X\sigma_Y，所以 r=1。

当完全负相关时，协方差 = -\sigma_X\sigma_Y，所以 r=-1。
当无线性关系时，协方差 ≈ 0，r \approx 0。

B. 距离

1. 欧氏距离(Euclidean Distance)

就是标准的直线距离。公式只是为了专业性，但是我觉得大概都能看明白。

d(x,y)=\sqrt{\sum_{k=1}^n (x_k-y_k)^2}

2. 曼哈顿距离(L1 norm)

因为纽约的地图呈现的样子，非常的标准，就是很多横平竖直的网格。就跟你过马路一样，你想要到对角线的对面去，但你得走两个斑马线才能安全到达。

d(x,y)=\sum_{k=1}^n |x_k-y_k|

3. 切比雪夫距离(L∞ norm)

那么，如果我们想知道在这个曼哈顿距离里，到底是哪段路最长，导致我们开车吃晚饭迟到，我们就要用到切比雪夫距离。

d(A,B) = \max |x_i - y_i|

4. 马氏距离 (Mahalanobis Distance)

这个是对欧式距离的优化。就很简单的例子，你考的语文分数和小明的差额是十分，你考的体育和小明差额也是十分。然是这两个的差额不能够直接对比不是吗？那么我们就要考虑这“十分“的环境意义是什么。

d_M(x,y)=\sqrt{(x-y)^\top \Sigma^{-1} (x-y)}.

如果难以理解，我给你个身高体重的差值，都是相差10，一个是10cm，一个是10kg。

那么如果一个圈代表着你身体突然的变化给你的吃惊程度，那么对于欧几里得距离来讲就跟图1 一样，增加10cm和增加10kg对于你的震惊程度是一样的。

但是我们都知道高10cm和胖10kg明显来讲，10cm会更明显一点。

那么因为这个更明显，所以我们的图从一个圆形，变成了一个椭圆形，因为你对于身高的敏感程度更高一点。

3. 数据预处理 (Data Preprocessing)

就是解决数据质量的问题。

1. 聚合-合并数据

2. 抽样-太多了，消化不了，啃一小口，但是啃的比较均匀，竖着吃三明治

3. 离散化与二值化 (Discretization & Binarization)

离散化：把连续变量转换成类别。

方法：等宽划分、等频划分、聚类划分。
例子：收入划分为“低、中、高”。

二值化：把变量转换为0/1。

例子：性别(男/女) → {0,1}。

4. 属性变换(Attribute Transformation)

标准化/归一化：消除不同属性的量纲影响。

我们刚才说的Pearson r。

z-score 标准化：减均值除标准差。
min-max 归一化：压缩到 [0,1]。
对数/指数/绝对值变换：缓解偏态、减少极值影响。

5. 降维 (Dimensionality Reduction)

就是太阳简化成火热的圆形，或者说，真空里的球形鸡来解决物理问题。
方法：(以后详细讲）

主成分分析 (PCA)

奇异值分解 (SVD)

其他：非线性降维、监督降维

6. 特征选择与构造（Feature Subset Selection & Feature Creation）

特征构造：默认的属性不好用，你新拼出来一个

例子：体重 / 身高² = BMI。

特征选择：去掉冗余和无关特征。

4. 信息论度量 (Information-Based Measures)

信息论的方法常用来衡量 不确定性 和 变量间的依赖关系。

就是衡量下这个数据到底有没有用。

比如你要送朋友礼物，你知道他喜欢苹果手机就很有用，但是知道他喜欢红色的有用程度就低一点。

1. 熵 (Entropy)

度量一个随机变量的不确定性。

H(X) = -\sum_{i=1}^n p(x_i)\log_2 p(x_i)

这玩意怎么理解呢，

就是当所有类别概率相等时，熵最大。抛硬币（公平）：H=1 bit。

如果抛两面相同的硬币（p=1）：H=0。这个时候熵最小。

2. 互信息 (Mutual Information, MI)

衡量两个变量共享的信息量。

I(X;Y) = H(X) + H(Y) - H(X,Y)

H(X,Y) = -\sum_{x,y} p(x,y)\,\log_2 p(x,y)

就是分别的混乱程度，减去他们一起的混乱程度。

有点类似联合概率。

举个例子：

	麦片=Yes	麦片=No	合计
牛奶=Yes	0.3	0.2	0.5
牛奶=No	0.1	0.4	0.5
合计	0.4	0.6	1.0

H(X)：只算“买不买牛奶”的不确定性。
H(Y)：只算“买不买麦片”的不确定性。

H(X,Y)：把四种组合情况都考虑：

(牛奶=Yes, 麦片=Yes) 概率 0.3
(牛奶=Yes, 麦片=No) 概率 0.2
(牛奶=No, 麦片=Yes) 概率 0.1
(牛奶=No, 麦片=No) 概率 0.4

H(X,Y) = -[0.3\log 0.3 + 0.2\log 0.2 + 0.1\log 0.1 + 0.4\log 0.4]

如果 X 和 Y 独立: H(X,Y)=H(X)+H(Y)，互信息=0。

如果 X 和 Y 强相关：H(X,Y)会小于 H(X)+H(Y)，说明“合在一起的不确定性”少了，互信息大。

3. 最大信息系数(Maximal Information Coefficient, MIC)（没发手算嗷）

Mic是刚才探讨的 相关系数 的升级版。

皮尔逊相关系数 只能看直线关系（x 增加，y 也大致增加/减少）。但如果关系是弯的、周期的、U 型的，正负变化互相抵消，结果可能接近 0。所以就会看不见非线性关系。
MIC 不挑剔：不管是直线、曲线、波浪形、U 型，甚至环形，它都能发现“这俩变量有关系”。
- 不强行假设关系是直线，而是 尝试用各种不同形状的网格 把数据划分。
- 在每个网格下，看数据点分布能不能“预测”对方（通过计算互信息）。
- 互信息不会要求是直线关系，只要有规律（X 能预测 Y），数值就高。
- 最后 MIC 会挑一个“最能体现规律的网格” → 给你一个 0–1 的分数。

M(a,b) = \frac{I(X;Y)}{\log_2(\min\{a,b\})}, \quad M(a,b) \in [0,1]

其实就是，散点图拿远了看，某些地方密集一点，某些地方散一点。然后如果密集的地方比较连续，也就是说密集的地方旁边也是密集的，那么大概率是有点规律在的。

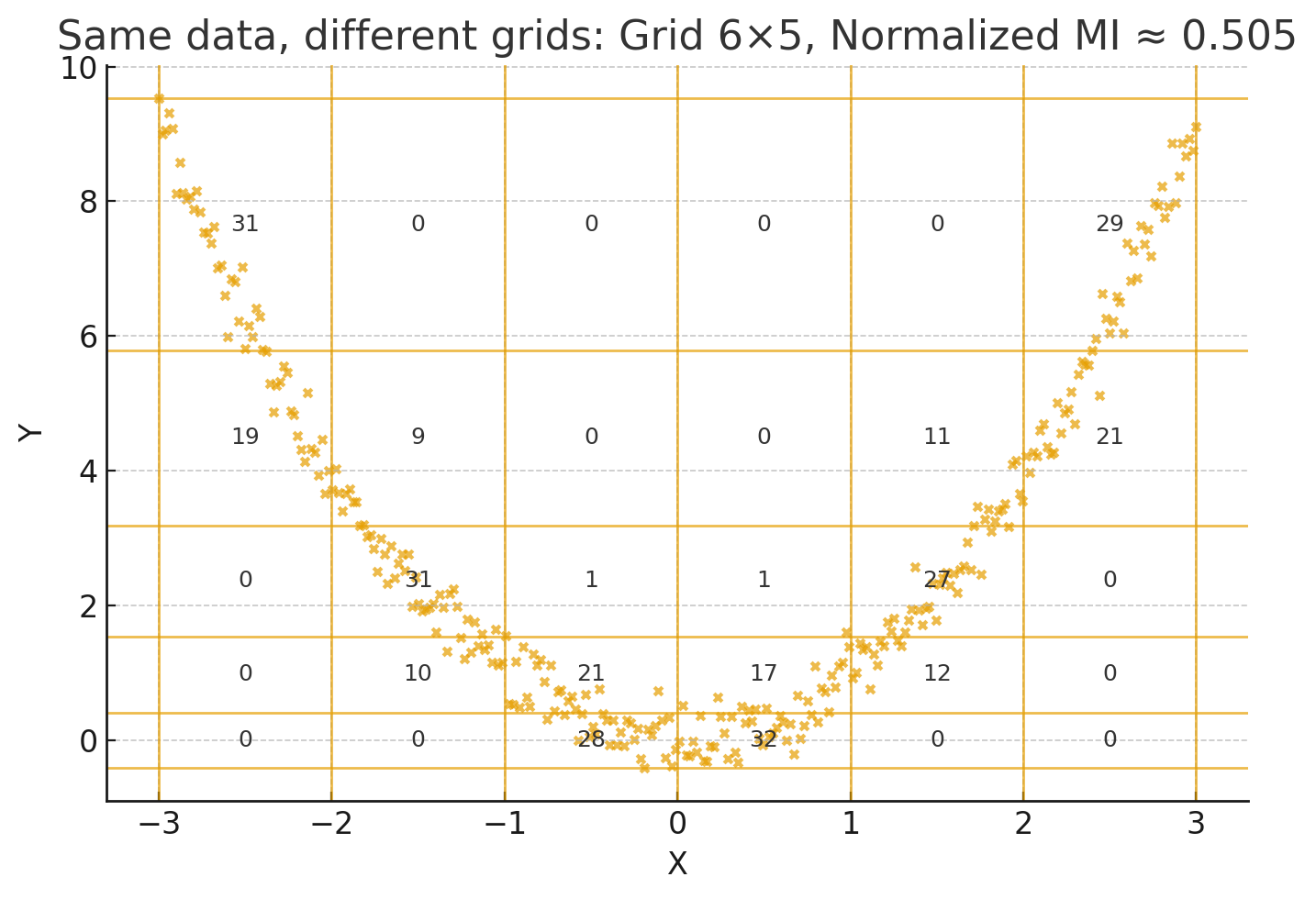
5. 比特（bit）

在信息论中，1 比特 = 能区分两种情况所需的信息量。

• Shannon 定义的信息量：

L(x) = -\log_2 P(x)

这里的 L(x) 就是描述事件 x 所需的“比特数”。

事件概率	信息量（比特）	含义
P(x)=1/2	1 bit	区分两个等可能事件（如抛硬币）
P(x)=1/4	2 bits	区分四种等可能事件
P(x)=1/8	3 bits	区分八种等可能事件

比特数 = log₂(可能情况数)或反过来，每比特表示一个“二选一”的信息单位”。

分享