我们终于开始说,准备怎么处理这些数据了。
1. 大的框架:监督与非监督,
A. 监督学习 (Supervised Learning)
-
定义:训练数据有输入 x 和对应输出 y(标签),目标是学习 f: x \mapsto y。
-
其实就是有题,有答案。
-
任务类型:
-
分类 (Classification):输出是离散类别(spam / not spam, 良性 / 恶性)。
-
回归 (Regression):输出是连续数值(预测房价、气温)。
-
-
核心思想:通过最小化训练误差 + 正则化,得到能在未见数据上泛化的模型。
-
例子:医学诊断(MRI 图像 → 肿瘤良性/恶性)。银行信用评分(客户特征 → 信用好坏)。
B. 非监督学习 (Unsupervised Learning)
-
定义:训练数据只有输入 x,没有标签 y。
-
有一堆答案,让你找答案的通用模版。
-
任务类型:
-
聚类 (Clustering):把相似样本分组(客户分群、基因表达模式)。
-
关联规则 (Association Analysis):挖掘共现模式(啤酒-尿布规则)。
-
降维 (Dimensionality Reduction):压缩表示,去除噪声,发现潜在结构(PCA)。
-
-
核心思想:通过度量相似性/结构,把数据组织起来。
-
例子:文本聚类(新闻自动分组)。市场细分(顾客行为分群)。
C. 半监督学习 (Semi-supervised Learning)
-
定义:数据中只有一部分有标签,大部分无标签。
-
老师给了模拟考试,然后还有模拟考试的答案,然后你找了去年的考试和前年的考试但是没有答案。你靠这些信息来尝试摸清老师考试的习惯。
-
典型场景:标注成本很高(医疗影像、语音转录),但无标签数据很多。
-
方法:利用无标签数据的分布 + 少量有标签数据 → 提升分类器性能。
D. 强化学习 (Reinforcement Learning, RL)
-
定义:智能体通过与环境交互,学习一种策略 \pi(a|s),以最大化长期回报(reward)。
-
打游戏的时候,你做的任何一个有效动作都会给你一个反馈的分数。比如击杀,辅助。然后你的目标是拿到游戏的最高分。
-
特点:
-
没有直接的正确标签,而是延迟反馈。
-
学习探索-利用平衡(exploration vs exploitation)。
-
-
例子: AlphaGo(围棋对弈)。自动驾驶(车辆控制策略)。
E. 其他类型
-
可以问问AI,因为很多我也不太了解,基本上是上面的互相结合什么的。
-
在线学习 (Online Learning):数据逐步到来时实时更新模型(如推荐系统)。
-
迁移学习 (Transfer Learning):在源任务上学到知识,迁移到目标任务(如用 ImageNet 预训练模型 → 医学影像识别)。
-
自监督学习 (Self-supervised Learning):通过数据内部结构生成伪标签(NLP 的 BERT 预训练,CV 的对比学习)。
2. 一些具体的训练方法
A. 分类(Classification)
a. 基本介绍
-
属于监督学习。(有题,有答案)
-
目标是最小化泛化误差(在未见过样本上的错误),而不仅是训练误差。(模拟题滚瓜烂熟,但是考试不一定拿高分。)
-
常用于典型输出是离散的类别(二分类、多分类)。
-
邮件 → 垃圾/正常;
-
医学影像 → 良性/恶性;
-
天文图像 → 星系类型。
-
b. 一般流程
-
学习(Learning / Training)
-
输入:带标签的训练数据 \{(x_i,y_i)\}。(有答案的模拟题)
-
目标:找到一个模型 f(x),能够把特征 x 映射到类别 y。(你在做题,尝试预判老师)
-
例子:学出一棵决策树、一个贝叶斯分类器、一张神经网络等。(之后会说的)
-
-
应用(Testing / Deployment)(真正考试)
-
输入:新的、没有标签的测试样本 x’。(真正考试题)
-
用学到的模型 f(x’) 输出预测标签 \hat y。(你的答案)
-
与真实标签对比,计算准确率、错误率等指标。(你的成绩)
-
B. 基础分类器(Base Classifiers)
先详细讲决策树。
a. Decision Tree(决策树方法)
-
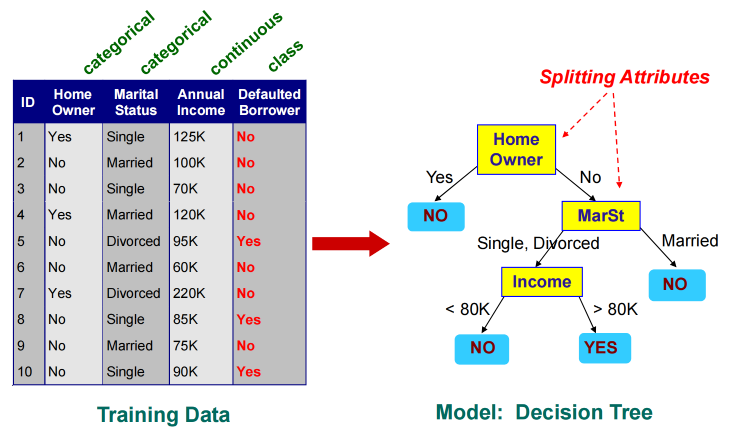
基于属性划分数据,形成树状规则。直观、易解释。
-
-
有点像流程图中的决策过程,也有点像if-else条件判断结构。
-
怎么生成?如上图,我们有三个attribute,那么你就从一个attribute开始分就行。
-
如何获得最好的树?是冗杂的对比计算。比如从每次分的效率最高的贪心算法,还是算互信息,最后都是看能否尽量完美的把测试集给分好了。
算法
-
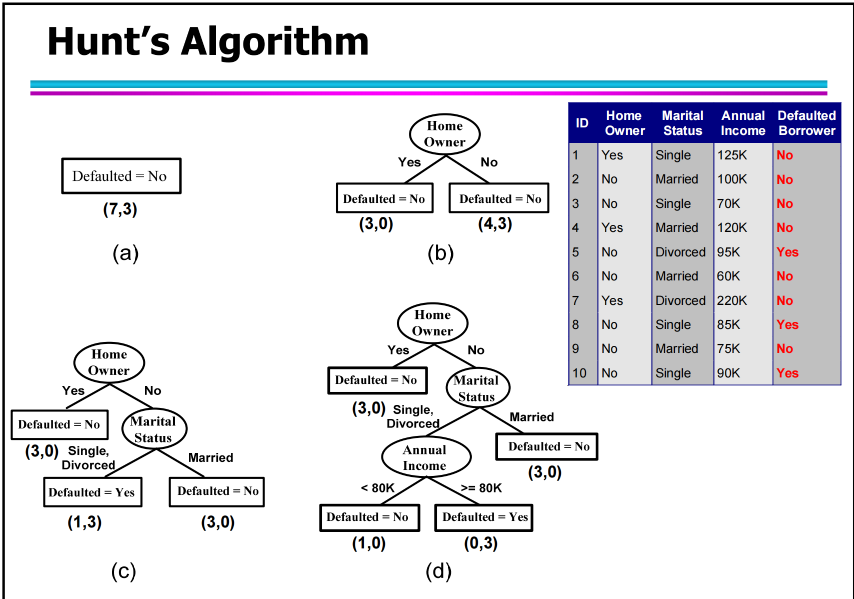
亨特算法
-
1. 如果 D_t 中所有记录都属于同一类别 y_t:→ 节点 t 变成叶子节点,类别 = y_t。
-
如图中的(b)的左边
-
-
2. 如果 D_t 中记录属于多个类别:→ 选择一个属性做测试条件,把数据划分为若干子集;
-
→ 对每个子集递归应用同样的过程。
-
如图中的(b)的右边
-
-
b. Rule-based Methods(基于规则的方法)
“if…then…” 形式的规则集合来分类。
c. Nearest-neighbor(最近邻法)
根据测试样本与训练样本的距离来决定类别(例如 k-NN)。
d. Naïve Bayes & Bayesian Belief Networks(朴素贝叶斯与贝叶斯网络)
基于概率和条件独立性假设。
e. Support Vector Machines (SVM)
通过寻找最大间隔超平面来划分类别。
f. Neural Networks, Deep Neural Nets(神经网络、深度神经网络)
多层非线性结构,强大但复杂。
C. 决策树的节点划分评估
a. 基尼指数(Gini Index)
-
p_i:在节点 t 上,属于类别 i 的比例。
-
c:类别的总数。
举个例子,先看这个,五个苹果,五个香蕉。那么Gini就是 1-(0.5^2+0.5^2)=0.5
这个时候是最混乱的上线 Gini=0.5。
决策树里怎么用
-
每次划分时,算法会计算“分裂前后”的 Gini 指数。
-
希望划分后,子节点的 Gini 越低越好(更纯)。
-
最佳划分 = Gini 减少最多的划分。
-
举个栗子 🌰
假设父节点有 10 个样本:6 个 No,4 个 Yes
Gini(parent) = 1 - (0.6^2 + 0.4^2) = 0.48
现在考虑用属性 “是否有房(HomeOwner)” 来划分:
-
左节点(有房):4 个 No,1 个 Yes → Gini=1-(0.8^2+0.2^2)=0.32
-
右节点(无房):2 个 No,3 个 Yes → Gini=1-(0.4^2+0.6^2)=0.48
加权 Gini:
-
Gini_{split} = \frac{5}{10}\cdot0.32 + \frac{5}{10}\cdot0.48 = 0.40
-
Gain = 0.48 - 0.40 = 0.08
-
如果其他属性的 Gain 更大,就会选择那个属性来划分。
-
二分类时,如果正例比例是 p,则
Gini = 2p(1-p)
b. 熵 (Entropy)
之前提到过,也是描述混乱程度。跟Gini 一样,越靠近0越好。
在决策树里的作用
-
每次划分,都希望 熵下降 → 子节点更纯。
-
信息增益 = 划分前熵 − 划分后熵(加权平均)。
c. 分类误差(Misclassification Error)
只看最多类别的比例。
Misclassification Error 就是在问:
“如果我只用这个节点里数量最多的类别去猜,那么我有多少比例会猜错?”
划分优劣度量的方法
1. 计算父节点 impurity (P)。
2. 计算子节点 impurity (M)(加权平均)。
3. 增益 (Gain) = P − M。选择增益最大的划分。
d. 增益率
-
增益是基于是基于不确定性的变化来的,但是有一个漏洞就是,如果我们分类特别多的话,那么极端情况下,分类数量等于我们的结果,那么熵的值直接等于0,而这样却没有任何意义了。
-
增益率修正了这一问题。
-
GainRatio = \frac{Gain}{SplitInfo},
-
SplitInfo = -\sum_{i=1}^k \frac{n_i}{n} \log_2 \frac{n_i}{n}
-
n_i:第 i 个子节点样本数
-
n:父节点样本数
-
-
增益率在保留“信息增益思想”的同时,惩罚了过度分支的划分。
D. 总结对比
顺序关系通常为:Entropy(p) > Gini(p) > Error(p)
-
构建树时:用 Gini(CART)或 Entropy(C4.5/ID3)。
-
剪枝或评估时:可用 Error 简化计算。
对于二分类问题
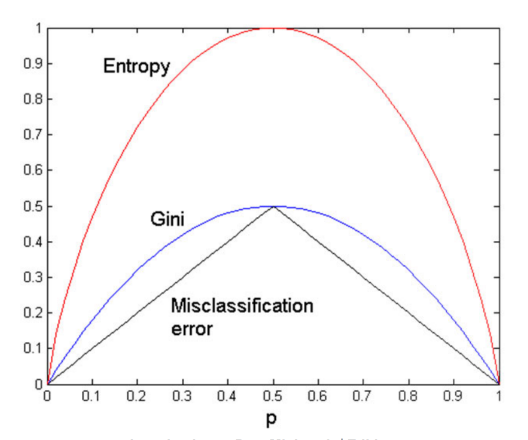
可以看出最敏感的是Entropy,熵。
E. 决策树的优缺点
优点(Advantages)
1. 构造代价低(Inexpensive to construct): 构建树只需局部计算(局部最优划分),计算效率高。
2. 预测速度快(Fast to classify unknown records): 预测时仅需从根到叶一路判断,复杂度接近 O(\log n)。
3. 易于解释(Easy to interpret): 可以转化为 “if…then…” 规则集合,透明直观。
4. 对噪声鲁棒(Robust to noise): 若采用适当剪枝方法,不容易被异常点误导。
5. 能处理冗余和无关特征(Handles redundant/irrelevant attributes): 冗余属性不会损害树结构;无关属性往往在划分时被忽略。
缺点(Disadvantages)
1. 贪心算法局限(Greedy nature): 决策树每一步选择局部最优划分,可能错过多个属性“协同”才能区分类别的情况。
-
例:两个特征单独都不能区分类别,但组合后能完美区分,树可能忽略它们。
2. 线性边界能力弱(Each decision boundary uses one attribute):
-
每个划分面都与坐标轴平行。
-
对“斜线型”或“复杂曲线型”边界的建模能力有限。
局限
问题背景:属性交互 (Feature Interaction)
有时,两个或多个属性单独看没用,但组合起来才有区分力。这类情况叫做 属性交互 (interaction between attributes)。
-
XOR(异或)示例: 假设有两个二元属性 X 与 Y:
-
-
若只看 X:正负样本各占一半 → 熵几乎为 1(最混乱)。
-
若只看 Y:一样 → 熵 = 1。
-
但如果看组合 X, Y:
-
当 X = Y → 正类
-
当 X \neq Y → 负类
-
-
完美可分!决策树通常在单属性层面划分,因此会忽略这种交互关系。
-
噪音的干扰
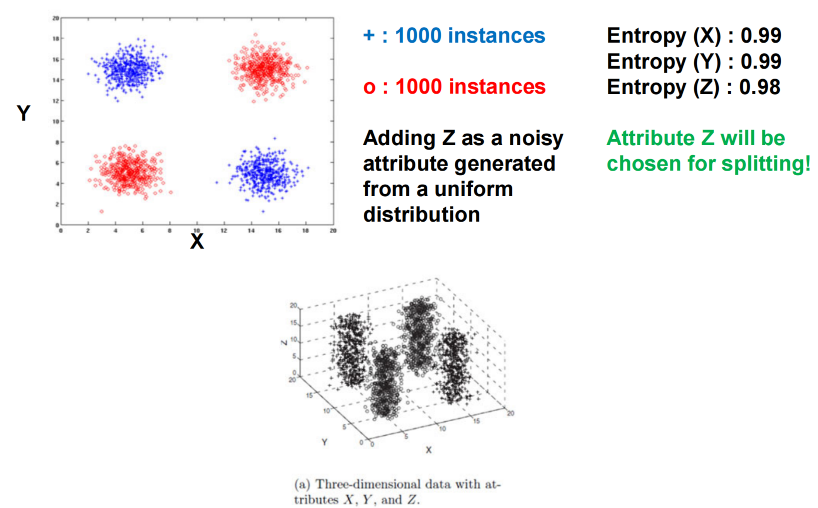
比如,我们能看出来,拿XY来分析是一个最好的方式。但是如果我们加入了噪音Z,那么Z就会因为微弱的优势导致我们分类方式产生偏移。其实也就是说,我们树的attribute在一开始的时候就需要是都有用的,甚至最好iid。