机器学习入门：4. 对模型的评估

1. 分类误差与泛化误差(Classification Error & Generalization Error)

A. 分类误差的三种类型

类型	定义	特点
训练误差 (Training Error)	模型在训练数据上的错误率。	越小说明模型拟合训练集越好。
测试误差 (Test Error)	模型在未见过数据上的错误率。	衡量泛化能力。
泛化误差 (Generalization Error)	理论上模型对整体数据分布的平均错误率。	通常用测试误差估计。

B. 分类对比

\text{Generalization Error} \approx \text{Expected Test Error} > \text{Training Error}

当模型简单时，三者接近。
当模型复杂时，训练误差趋近 0，但测试误差反而上升（过拟合）。

错误率 (error rate) = 错误分类数 / 总样本数
准确率 (accuracy) = 1 − 错误率

C. 训练误差 \leq 泛化误差

训练误差（training error）永远低估模型的真实错误率（泛化误差）。

模型是为了拟合训练数据而“优化”的
- 决策树、神经网络、SVM……都在“训练集”上反复调整参数。模型自然会在训练样本上表现越来越好。
- 但这些调整可能过度匹配噪声 → 在新数据上失败。
训练误差缺乏独立性
- 训练集和模型之间存在信息泄露（data reuse）：模型“见过这些样本”。
- 因此训练误差反映的是“拟合效果”，而不是“预测能力”。

2. 欠拟合与过拟合（Underfitting vs Overfitting）

A. 两者对比

类型	定义	表现	原因
欠拟合 (Underfitting)	模型太简单，无法捕捉数据规律。	训练误差高，测试误差也高。	模型能力不足（例如线性模型拟合非线性关系）。
过拟合 (Overfitting)	模型太复杂，把噪声也学进去。	训练误差很低，测试误差上升。	模型容量过大 + 数据有限。

本质的问题是，你得考虑泛化。你通过模拟考试弄出来的东西，真正考试的时候不一定这么出。你把模拟考试的答案背下来直接去写真实考试，这就是过拟合。但是你模拟考试都没弄明白，那就是欠拟合。泛化能力才是关键。

B. 误差曲线

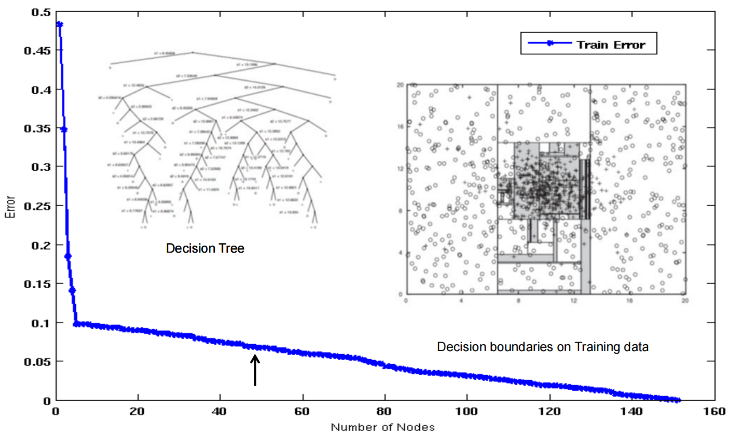
你可以看出来，模型的复杂度对拟合的帮助在一个临界值之后快速下降。

误差曲线形状

\text{模型复杂度} ↑ \Rightarrow \begin{cases} \text{训练误差(Training Error)} ↓ \\ \text{真实误差(Test Error)} ↓ \text{ then } ↑ \end{cases}

即 U 形关系：

起初增加复杂度有助于减少误差。

超过最佳点后，模型开始学习“噪声”。

C. 过拟合的原因

a. 数据不足 (Insufficient Training Data)

核心结论训练数据量越大，过拟合风险越低。
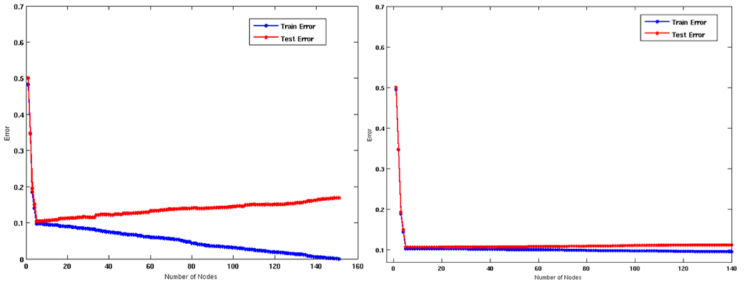
第二张图是两倍数据量的结果。

b. 模型太复杂 (Excessive Model Complexity)

其实就是所谓的读书读太杂了，然后又不能整合，看到核心问题。

决策树节点过多、神经网络层太深、参数过多都会导致：

高方差 (variance)；
模型过度响应训练集的特定结构。
复杂模型拥有更高的“容量 (capacity)”：能拟合更多模式，包括错误模式。

c. 多重比较问题 (Multiple Comparison Procedure)

“在足够多次尝试下，总能找到一个看似完美但其实随机的结果。”

—— 不知道是谁

举例：如果我们测试100个属性，即使所有属性与类别完全无关，也可能偶然出现一个属性“看起来”能完美划分训练样本。

这是随机波动被误认为规律的典型情况。类似反复试错直到“碰巧”猜对一次。

想象有 50 个股票分析师：

每人随机预测市场涨或跌。
第一周后，大约 25 人预测对。
第二周，这 25 人再随机预测，又有约 12–13 人连对两次。
到第 6 周，可能有一个分析师“连续6次预测对”。→ 看起来他“超神”，但实际上是随机概率的产物。

D. 解决方法

方法	作用
使用验证集	在独立数据上确认结果是否真实有效。
使用交叉验证 (cross-validation)	多次分割数据，减少偶然性。
采用显著性校正	例如 Bonferroni 或 FDR，防止假阳性过多。

验证集，一般就是82分，百分之八十用来训练，百分之二十用来验证。

那么怕这个验证多了出现问题，所以一般我们随机切割这个东西，比如随机分十个八二分，我们就有了交叉验证。

显著性矫正就是，对于交叉验证来说，每次的错误不能累加，比如十次交叉验证之后，你这个错误率也得处以10来平衡。

3. 模型选择与复杂度惩罚(Model Selection & Complexity Penalty)

模型越复杂，训练误差越低, 但是过拟合的风险就越高；但为了防止过拟合，我们要在误差与复杂度之间权衡。

A. 方法一：使用验证集评估模型

将训练集拆成：子训练集（用于拟合参数）；验证集（用于比较不同模型的性能）。选出在验证集上错误率最小的模型。

这种做法本质上用经验泛化误差来评估不同模型复杂度的好坏。

B. 方法二：在目标函数中加入复杂度惩罚

复杂度惩罚项可以取决于：

模型的自由参数数量（参数越多，惩罚越大）；
树的深度、节点数等结构指标；
模型的不确定性或容量（capacity）。

名称	公式（简化）	含义
AIC (Akaike Information Criterion)	AIC = 2k - 2\ln(L)	k=参数数目；惩罚模型复杂度
BIC (Bayesian Information Criterion)	BIC = k\ln(n) - 2\ln(L)	惩罚更强，更保守
Structural Risk Minimization (SRM)	R_{emp} + \lambda \cdot \text{Complexity}	来自奥卡姆剃刀法则。

C. 悲观误差估计

Structural Risk Minimization (SRM) 对应着 奥卡姆剃刀法则：“如无必要，勿增实体。”

在能实现相同效果的时候，优先选择更简洁的模型。

\text{Generalization Error(Model)} = \text{Training Error(Model)} + \alpha \times \text{Complexity(Model)}

那么对应到选择树上，我们考虑的是，如果减去某项分类，到底会不会优化?

err_{gen}(T) = err(T) + \Omega \times \frac{k}{N_{train}}

err(T)	树在训练集上的经验错误率（Training Error）
k	叶节点数（leaf nodes）
N_{train}	训练样本总数
\Omega	超参数（类似前面讲的 \alpha，代表“增加一个叶子的代价”）
err_{gen}(T)	对树的“泛化误差”的悲观估计（Pessimistic Estimate of Generalization Error）

a. 案例

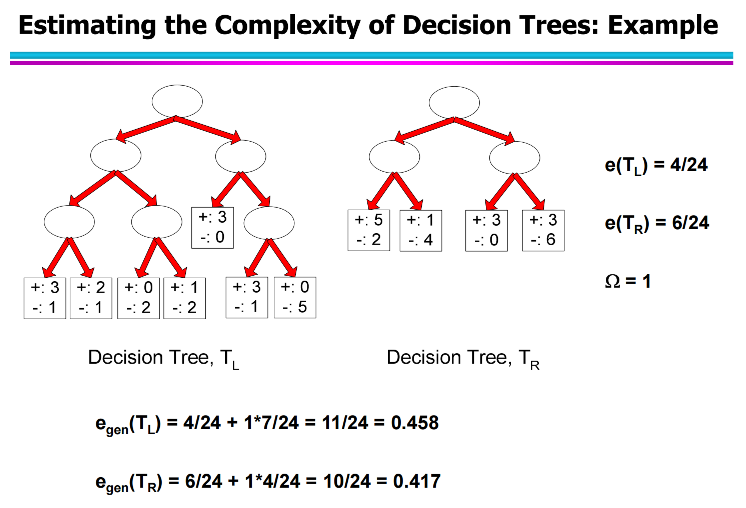
比较两棵树：

Tₗ（左树）：更复杂（更多叶子）
Tᵣ（右树）：更简单（更少叶子）

两者训练样本总数都是 N_{train}=24，惩罚系数设为 \Omega = 1。

b.计算训练误差 err(T)

看右边标注：

这个是每个方框内较小的数字的相加。

e(T_L) = 4/24 = 0.167
e(T_R) = 6/24 = 0.25

也就是说：

• 左树更复杂，训练误差更低；

• 右树更简单，训练误差略高

c. 确定叶子数 k

观察图示：

• 左树 T_L：最底下红框共 7 个叶子

• 右树 T_R：只有 4 个叶子

所以：

k_L = 7, \quad k_R = 4

d.代入“悲观误差”公式

err_{gen}(T) = err(T) + \Omega \times \frac{k}{N_{train}}

其中 \Omega = 1,\; N_{train}=24。

左树 T_L

err_{gen}(T_L) = \frac{4}{24} + 1 \times \frac{7}{24} = \frac{11}{24} = 0.458

右树 T_R

err_{gen}(T_R) = \frac{6}{24} + 1 \times \frac{4}{24} = \frac{10}{24} = 0.417

e. 结果解读

树	训练误差	叶节点数	泛化估计 (悲观误差)	结论
左树 T_L	0.167	7	0.458	更复杂但泛化差
右树 T_R	0.25	4	0.417	更简单但泛化更好 ✅

\text{泛化误差} = \text{经验误差} + \text{复杂度惩罚}

D. C4.5 的方法

类似的道理，但是换一些参数罢了。

\hat{E} = \frac{ e + 0.5z^2 + z\sqrt{\,e - e^2/n + 0.25z^2\,} }{n + z^2}

e = 节点中的错误样本数；
n = 节点样本总数；
CF = 置信因子（C4.5 默认 0.25，对应 z = 0.69）。

4. 模型优化之”减树枝“

A. Pre-Pruning（预剪枝 / Early Stopping Rule）

在建树过程中提前停止扩展节点，防止树长得太深。也叫 “早停法”。它在模型构建阶段就决定“不再往下分”。

a. 典型停止条件

1. 所有样本属于同一类→ 节点已经纯净，无需继续分裂。

2. 所有属性取值完全相同→ 再分也不会带来信息增益。

b. 更严格的停止条件（Practical Rules）

条件	含义
样本数太少	若节点中样本数 < 阈值（如 min_samples_split ），停止。
属性与类别独立	用 χ² 检验检出“无关联”，则不划分。
纯度提升太小	若信息增益或 Gini 下降 < 阈值 (min_impurity_decrease) ，不划分。
泛化误差已稳定	若预计的 generalization error 低于某个阈值，停止。

优点	缺点
训练速度快、树更小	可能错过潜在有用的分裂（贪心）
可直接在训练阶段控制复杂度	一旦停早，无法“反悔”调整

B. Post-Pruning（后剪枝 / Subtree Replacement）

先把树完整地长出来，再从底部往上逐步“修剪”不必要的分支。又称 Subtree Replacement（子树替换）。

操作步骤

1. 先构建完整树（即使可能过拟合）。

2. 自底向上检查每个节点的子树：临时将该子树剪掉，用一个叶子节点替代。

3. 计算剪前剪后泛化误差（或验证误差）：

如果剪枝后误差不变或下降 → 确认剪枝。
否则恢复原子树。

4. 新叶节点的类别标签由该子树中样本的多数类决定。

比预剪枝更稳健	先让模型充分学习，再决定哪些分支真的必要
通常能获得更优的泛化性能	是 C4.5、CART 默认使用的策略

C. 对比总结

特性	预剪枝 (Pre-pruning)	后剪枝 (Post-pruning)
时机	树生成时	树生成后
控制方式	阈值条件提前停	利用验证或误差评估
速度	快	稍慢
泛化能力	一般	通常更好
代表算法	ID3 (限深度)	C4.5, CART

总结

预剪枝：贪心、快速、风险是“停早”；
后剪枝：先放手学，再审慎减，泛化更强；
实际上现代树模型（如 Random Forest, GBDT）都默认包含某种后剪枝或正则化机制。

4. 最小描述长度原则(Minimum Description Length, MDL)

A. 总编码长度最短

最优模型 = 能最简洁地解释数据的模型。也就是说，我们希望选择那个总编码长度最短的模型

L_{\text{total}} = L(\text{Model}) + L(\text{Data | Model})

其中：

L(\text{Model})：编码模型本身需要的“长度”（越复杂的模型越长）；
L(\text{Data | Model})：在给定模型下，描述剩余误差（data residuals）所需的“长度”。

目标是让两者之和最小。

如果模型太简单 → L(\text{Model}) 很短，但 L(\text{Data | Model}) 很长（模型解释不了数据，残差多）。

• 如果模型太复杂 → L(\text{Model}) 很长（要描述太多参数、分支），即使残差短也不划算。

• MDL 找的是两者平衡点。

👉 这和我们之前的：

\text{Generalization Error} = \text{Training Error} + \text{Complexity Penalty}

完全一致，只是换了“信息论”语言。

B.在决策树中的应用

L(\text{Model})：

描述整棵树的结构（每个节点用哪个属性、阈值、分支数）。
L(\text{Data | Model})：对叶节点中的错误样本编码（多少条样本被错分）。

剪枝策略：

若剪掉某个子树能使 L_{\text{total}} 变短 → 就剪。
否则保留。

C. 例子

还是用上面的例子

左树 T_L：节点结构与数据分布

叶编号	标签框	正类 (+)	负类 (−)	节点样本总数	误分数	经验错误率
1	+3 −1	3	1	4	1	0.25
2	+2 −1	2	1	3	1	0.33
3	+0 −2	0	2	2	0	0.00
4	+1 −2	1	2	3	2	0.67
5	+3 −0	3	0	3	0	0.00
6	+1 −1	1	1	2	1	0.50
7	+0 −5	0	5	5	0	0.00
合计	–	–	–	–	5	–

右树 T_R：节点结构与数据分布

叶编号	标签框	正类 (+)	负类 (−)	总数	误分数	经验错误率
1	+5 −2	5	2	7	2	0.29
2	+1 −4	1	4	5	1	0.20
3	+3 −0	3	0	3	0	0.00
4	+3 −6	3	6	9	3	0.33
合计	–	–	–	–	6	–

树	叶子数 k	总误分 e	结构复杂度	错误数	特征
T_L	7	5	较复杂	少	“大树”拟合得好
T_R	4	6	简单	稍多	“小树”更简洁

应用 MDL 原理对比, 我们假设：

每个叶子的结构编码成本 c 比特；
每个误分样本的代价 b 比特。
MDL 的总编码长度：我们设置了不同的c 和 b 来对比想要的效果。

情形	c	b	L(T_L)	L(T_R)	更优树
注重简洁（c 大）	5	1	5×7+1×5=40	5×4+1×6=26	T_R
注重准确（b 大）	1	5	1×7+5×5=32	1×4+5×6=34	T_L
折中情况	2	2	2×7+2×5=24	2×4+2×6=20	T_R

5. 模型评估方法(Model Evaluation and Model Selection)

这个在上一章我们就稍微说了一下，但是我们这一次复习加上添加一些新的东西。

建立分类模型后，我们要回答两个核心问题：

1. 模型泛化得好吗？→ 评估它在未见数据上的表现。

2. 哪个模型最好？→ 对比不同参数/算法/复杂度下的泛化性能。

A. 留出法(Holdout Method)

将数据随机划分为两部分：

Training set（训练集）——用于拟合模型。
Test set（测试集）——用于估计泛化误差。

常用比例：

70% 训练 / 30% 测试
80% 训练 / 20% 测试

问题

结果依赖于随机划分；
如果样本较少，测试集太小 → 估计方差大；
如果测试集太大 → 训练数据不够。

B. 交叉验证法(Cross-Validation)

a. k-Fold Cross-Validation

1. 将数据随机划分为 k 个等大小子集。

2. 每次取其中 1 份作验证集，其余 k-1 份作训练集。

3. 重复 k 次，每次验证集不同。

4. 最终性能 = 平均验证误差。

常用取值：k=5 或 k=10。

优点

利用全部数据进行训练与验证；
减少划分偶然性；
更适合小样本场景。毕竟你要跑5-10遍。

b. k-fold的变形

名称	特点
Leave-One-Out (LOOCV)	每次留出一个样本作验证；适用于样本很少时。
Stratified k-Fold	保持每折的类别比例与整体一致；用于类别不平衡数据。
Repeated k-Fold	多次随机分折取平均；进一步减少方差。

C. 自助法(Bootstrap Method)

从原始数据集中有放回地随机抽样 n 次（与样本总数相同）。

约 63.2% 的样本被抽到（训练集）；剩下约 36.8% 的样本作为“袋外样本 (out-of-bag)”用于测试。
对多次自助样本计算误差，再取平均。

相当于你在复制里面的数据嘛。然后相当于放大了里面的微小趋势。

D. 嵌套交叉验证(Nested Cross-Validation)

当我们需要模型选择 + 性能评估同时进行时（例如调超参数）。

外层交叉验证：用来评估模型最终泛化性能。

内层交叉验证：用来在不同超参数或模型之间进行选择。

外层划分成 K 折。
在每一折中，用内层交叉验证挑选最佳模型/参数；再在外层验证集上计算泛化误差。

最终外层平均误差 = 模型的可靠估计。

E. 评估指标（Evaluation Metrics）

指标	定义	适用场景
Accuracy	正确预测数 / 总数	类别平衡时使用
Error Rate	1 − Accuracy	同上
Precision	\frac{TP}{TP+FP}	关注“预测为正”中有多少真的正
Recall / Sensitivity	\frac{TP}{TP+FN}	关注“真正例被识别的比例”
F1 Score	2 \times \frac{PR}{P+R}	综合考量精确率与召回率
ROC / AUC	面积越大越好	模型整体区分能力

目的	方法	特点
快速评估	Holdout	简单但不稳定
稳健评估	k-Fold CV	推荐默认方法
小样本估计	Bootstrap	利用重复抽样
调参 + 评估	Nested CV	防止信息泄露
指标层面	Accuracy, AUC, F1	针对任务需求选择

分享