贝叶斯决策规则 & 最大后验概率(Bayesian Decision Rule & MAP)
你是一个信用卡审批员。来两个申请人(A 和 B),你要判断:这个人会不会违约?
类别就两个:Yes = 会违约,No = 不会违约。
但你不能直接看到未来,只能看到一些特征,比如:
-
收入高低
-
是否已婚
-
是否有退税记录
你有历史数据:以前成千上万客户的特征和结果。那我们该怎么用这些信息去判断“新客户”属于哪个类别呢?
A. 贝叶斯方法
我们想要计算:P(\text{会违约} \mid \text{这些特征}),意思是“在这些特征条件下,这个人会违约的概率有多大?”
但我们往往没有直接的 P(\text{会违约}\mid\text{特征}),我们能统计到的是历史数据中的:
-
P(\text{特征}\mid\text{会违约}):在违约人群中,这种特征出现的概率
-
P(\text{会违约}):有多少比例的人会违约(先验概率)
贝叶斯定理告诉我们:
意思是:“我们只要算出在违约人群中出现这种特征的概率,再乘上违约率,就能得到一个代表‘后验’的分数。”
\propto 意思是正比于。
比如你判断“明天下雨”:
P(\text{雨}\mid\text{看到乌云})\propto P(\text{看到乌云}\mid\text{下雨})\times P(\text{下雨})
-
P(\text{下雨}):这个城市的常年下雨率
-
P(\text{看到乌云}\mid\text{下雨}):下雨天时看到乌云的概率
-
你不需要管分母 P(\text{看到乌云}),因为两种情况都一样。
B. 背后原理
条件概率定义是:
意思是,“在事件 B 已经发生的情况下,A 同时发生的概率等于 A、B 同时发生的概率除以 B 的概率。”
两边都有 P(A \cap B)。于是我们把它们联系起来:
P(A \mid B) P(B) = P(A \cap B) = P(B \mid A) P(A).
那么你可以看到,通过交集,条件和事件可以相互交换,这就给了我们可以操作的空间。
还是刚才的例子:
设:A = “今天下雨” B = “我看到乌云”
那么:P(A \mid B) = \frac{P(B \mid A) P(A)}{P(B)}
解释:
-
P(A):平时下雨的比例(先验)
-
P(B \mid A):下雨天看到乌云的概率(条件概率)
-
P(B):总体上看到乌云的概率(包括没下雨时)
-
结果 P(A\mid B):看到乌云后下雨的概率(后验)
C. 先验与后验
a. 先验(prior)
先验 是在看到任何数据之前,我们原本对事情的主观信念或历史概率。
例如:在这城市,平时下雨的概率是 0.3。
这就是先验 P(\text{rain}) = 0.3。
b. 后验(posterior)
后验 在得到新证据之后,我们更新过的信念。
例如:现在天上有乌云 ☁️那么在这种“有乌云”的信息下,下雨的概率就变了:
P(\text{rain} \mid \text{cloudy}),这就是后验。
贝叶斯属于后验。
c. 拓展与总结
d. 贝叶斯的重新理解
贝叶斯定理告诉你一个从“先验”更新为“后验”的数学法则:
你原来有一个“先验” P(A);当你看到新证据 B 时,你用贝叶斯公式去“修正”它,得到更新后的“后验” P(A|B)。
这整个更新的过程,就是 Bayesian Updating(贝叶斯更新)。而这个更新规则,就是“后验定理”。
再举个例子,主要是我当时理解这个理解了很久,不难,就是需要重新建立模型。
想象你是医生:
-
先验:病人得癌症的总体概率是 1%。
-
新证据:病人筛查阳性。
-
你要更新判断:病人真的有癌症的概率是多少?
这个“更新”就是通过贝叶斯定理算:
所以贝叶斯定理是一个把旧信念更新为新信念的规则,更新完得到的概率叫“后验概率”,因此整条公式就自然被称作“后验定理”。
D. 应用贝叶斯
a. 决断公式MAP(Maximum a Posteriori)
给定特征向量 X=(X_1,\dots,X_d),要判别类别 Y\in\{1,\dots,C\}。贝叶斯思想:选择使后验概率最大的类别
\hat y \;=\; \arg\max_{c\in\{1,\dots,C\}} P(Y=c\mid X) ,P(Y=c\mid X) \;=\; \frac{P(X\mid Y=c)\,P(Y=c)}{P(X)}。
叽里咕噜什么意思呢?基于X=(X_1,\dots,X_d),我去判断属于什么 Y, 类型是从 {1,...,C}。我们分别计算每一种类别基于特征的可能性, P(Y=c\mid X),然后 \arg\max_{c\in\{1,\dots,C\}}代表从这个范围里找到概率最大的 Y 类。
总结来说就是:根据特征,计算每个类别的“后验概率”,选出最可能的那个。
b. 条件独立假设(Conditional Independence)
我们看到计算: P(X|Y)=P(X_1,X_2,X_3|\;Y), 理论上应该考虑特征之间的联合分布,也就是:
P(X_1,X_2,X_3|\;Y),为了简化,我们假设:在给定类别 Y 的情况下,各个属性 X_1,X_2,\dots,X_d 之间条件独立。
形式化地写:
那么对于很多参数的情况下,我们只用一个一个计算参数然后将其相乘就好了。
c. 连续样本处理
我们用分段处理方法去统计,然后套入正态分布公式来辅助计算P值。
d. 0值处理
因为乘法的原因,如果任何一个中间项目变成了空项目,那么我们有可能就会出现0值,那么就会导致整个结果变成0。
为了解决这个问题,我们的方法是对离散特征 X_j 的每个取值 c,把类内计数 n_c 加 1:
其中 n 是该类样本总数,v 是该特征的可能取值数。这样即使训练集中没见过,也会得到一个很小但非零的概率。
2. m-估计(m-estimate)(拉普拉斯的推广):
p 是先验(常取均匀分布 1/v),m 控制“先验权重”。当数据很少或极不平衡时更稳。
e. 总结
优点
1. 抗噪声:个别离群点不太影响整体判断。
2. 能处理缺失值:做条件概率估计时可忽略缺失项。
3. 对不相关特征鲁棒:少量“无关维度”不会显著拖累效果。 
• 主要风险/缺点
• 冗余或强相关特征会违背“条件独立”假设,性能下滑;这时可考虑更灵活的模型(下一节的 BBN)。 
但是当属性之间明显相关时(比如一堆高度相关的计数词频),NB 的独立性被破坏 → 需要别的办法。
E. 贝叶斯优化(Bayesian Belief Networks)-贝叶斯网络
思路很简单,传统的朴素贝叶斯预设各个参数是不相关的独立参数。但是当我们的参数并不独立的时候,我们可以提前处理参数让其变得独立。其中一种方式就是把相关的参数放成一组,然后再进行计算。
那么我们就有了逻辑树加上贝叶斯。
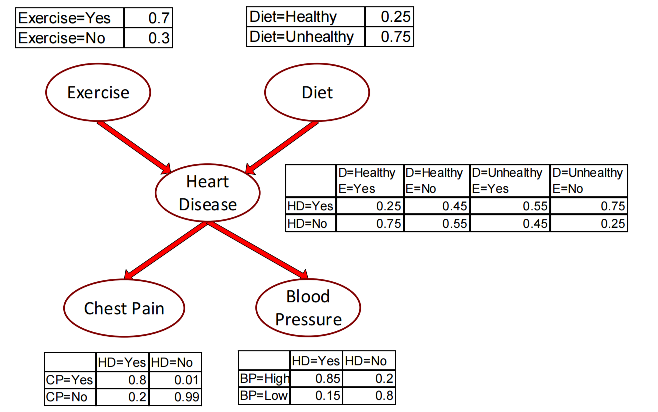
比如,我们想知道的是中间的心脏病,然后我们通过逻辑分析知道了
-
锻炼和饮食会影响心脏病。
-
心脏病会影响胸疼和血压。
那么我们遵循刚才的思路继续推进,锻炼和饮食我们就可以合并成为一个来处理,然后心脏病单独作为结果,胸痛和血压作为两个单独因子,因为他们相对独立。
那么我们假设病人 P(HD{=}Yes \mid E{=}No,D{=}Yes,CP{=}Yes,BP{=}High) 是这么个情况,我们怎么处理?
我们想要的其实是:P(HD\mid E,D,CP,BP)
根据贝叶斯公式:
根据 贝叶斯网络的分解规则(每个节点只依赖它的父节点):
代回上面的贝叶斯公式
在这个式子里,P(E) 和 P(D) 不依赖 HD,对比 “HD=Yes” 和 “HD=No” 时它们是同一个常数因子,可以直接忽略。
于是剩下的部分:
带入数值
归一化

