1. Rule-Based Classifier 的核心思想
A. 基于规则的分类是什么?
核心就是如果满足什么条件,就怎么怎么样。
IF <条件> THEN <类别>这种规则由两部分组成:
-
前件 (antecedent):条件部分(IF …)
-
后件 (consequent):预测的类别(THEN …)
B. 与决策树的渊源
但是其实这个rule based特别像我们之前说的决策树不是吗?
其实它就是另外一种决策树,只不过决策树一般来说是靠属性来分类的,而基于规则则是更为灵活的将属性组合起来。
也就是说属性现在可以组合成为新的属性罢了。而且作为组合的元素可以出现不止一次。
C. 对于规则的评估方式
a. 覆盖性
一条规则 r covers 一个样本 x,当且仅当这个样本的所有属性都满足规则 r 里的条件。
也就是说,如果一个规则完美的覆盖了这个样本,而且没有其他规则去解释它,那么就符合一个覆盖。
但是并不是都这么完美,所以我们可以计算一个规则的覆盖率。
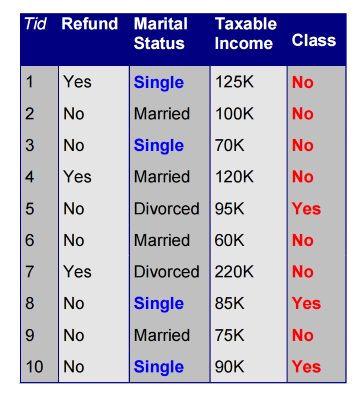
b. 正确率,就是正确率
比如说,此时的规则 (status=Single)\to \ No就是 百分之40 的覆盖率和百分之50的正确率。
c. 互斥(Mutually Exclusive)
任意两个规则不应该同时覆盖(cover)同一个样本。
也就是说:
-
一个样本 x 最多只能命中一条规则;
-
不会出现同时满足 R_1 和 R_2 的情况。
d. 完备(Exhaustive)
所有样本都应当至少被一条规则覆盖。不能有样本落在“没有任何规则命中的空白区”。
如果怎么分都有漏网之鱼,那么就用默认规则。
D. 规则冲突
假如我们的一个测试对象同时满足两条甚至更多的分类标准,比如经典的鸭嘴兽问题,它到底算什么动物?
a. 无序规则集(Unordered Rule Set)
所有规则都是平等的;匹配多条,就“投票决定”。
具体做法:
-
把所有匹配的规则都找出来;
-
看它们各自预测的类别;
-
最常见的类别获胜(多数投票)。
优点:
-
简单;
-
对单条规则的错误不敏感。
缺点:
-
如果有冲突、规则数多,结果可能不稳定;
-
每次预测都要检查全部规则,效率略低。
b. 有序规则集(Ordered Rule Set)
给每条规则一个优先级(顺序),一旦匹配成功,立刻停止检查。
优点:
-
规则执行效率高;
-
容易控制优先级(先一般性、后特例)。
缺点:
-
规则顺序非常重要;
-
如果顺序错了,预测会全乱。
c. 默认规则 (Default Rule)
用来处理没被任何规则覆盖的样本。
2. 规则生成(Rule Generation)
在 Sequential Covering / learn-one-rule 过程中:
-
我们通常选择一个目标类(正样本类),
-
然后去找一条规则,尽量覆盖正样本、排除负样本。
A. 核心思想(Direct Method)
逐条生成、逐步覆盖(Sequential Covering)
简单讲:
-
一次不生成全部规则;
-
而是每次找到一条“好规则”(能抓到最多正样本、最少负样本),然后把这条规则覆盖掉的数据从训练集中移除;
-
再在剩下的数据上重复;
-
直到所有正类样本都被至少一条规则覆盖。
B. learn-one-rule(D)
每次在当前规则的条件集合上:
1. 从一个“空条件”开始;
2. 每次添加一个条件(attribute test),
让规则的 accuracy 尽可能提升;
3. 当再加条件不能显著提升效果时,停止;
4. 最后得到的那条规则,就加入规则集。
一种是逐渐复杂,另外一种是逐渐简化。
C. 信息增益(FOIL 的信息增益)
用来在 learn-one-rule() 的 Grow 阶段评估“往规则里再加一个条件 A 值不值”。
现在有一条“当前规则” R_0(它的前件可能是空的 {}),
-
尝试再加一个条件 A 得到新规则 R_1 = R_0 \land A。
-
p_0,n_0: R_0 覆盖到的正/负样本数
-
p_1,n_1: R_1 覆盖到的正/负样本数
-
FOIL 增益定义为
括号里是“精度(precision)提升的对数”,前面的 p_1 是“覆盖到多少正例”的权重。既想更准,也要抓住足够多的正例。
\frac{p}{p+n} 就是“当前规则的精度”(覆盖样本里有多大比例是真的正类)。
• 新旧精度的 \log 差表示“信息提升/压缩节省”,乘上抓到的正例数 p_1 表示“这次提升影响到了多少正例”。
• 所以 高增益=精度升得多且抓到的正例也多。只涨一点精度却只覆盖 1 个正例,得分就不会高。

