机器学习入门 8: 支持向量机 SVM
一、核心思想
SVM 的目标是:
找到一个能最大化类别间隔(margin)的分割超平面。
换句话说,它不仅仅是把两类数据分开,而是希望“分得最开”,并且尽量让边界尽可能远离两边的样本点。
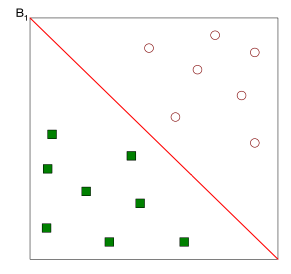
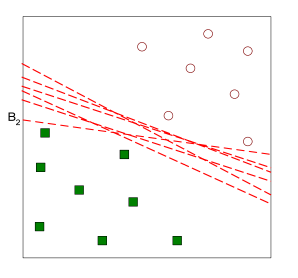
如图,这是一个二维平面的划分。我们可以划出很多类似的分割线。
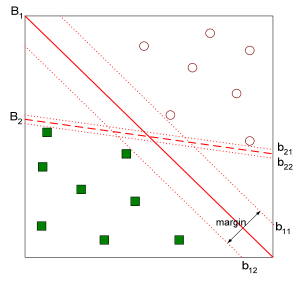
但是我们画出的分割线可以越宽越好。
二、线性 SVM
1️⃣ 模型形式
超平面方程为:w \cdot x + b = 0其中 w 是法向量, b是偏置。
预测规则:
2️⃣ 间隔(Margin)
间隔的宽度为:\text{Margin} = \frac{2}{\|w\|}
最大化间隔等价于最小化\frac{1}{2}\|w\|^2。
3️⃣ 约束条件
对于每个样本 (x_i, y_i),要求:y_i(w \cdot x_i + b) \ge 1

三、优化问题(线性可分)
目标函数:\min_{w,b} \frac{1}{2}\|w\|^2
约束:y_i(w\cdot x_i + b) \ge 1, \ \forall i
这是一个 凸优化问题,可用 Lagrange 乘子法 求解。
四、非线性情况(就是可以容忍一些错误划分)
1️⃣ 问题
数据往往不是线性可分的。此时我们引入 松弛变量 \xi_i:
新的目标函数:
其中 C 控制对错误分类的惩罚力度。我们需要最小化它。
不断最小化的过程,也是不断调优的过程。
五、非线性 SVM 与核技巧(Kernel Trick)
如果原始空间无法线性分割,我们可以把数据 映射到高维空间:
2. 在高维空间中再寻找线性超平面。
但直接映射会很耗计算,因此使用核函数 K(x_i, x_j) = \Phi(x_i)\cdot\Phi(x_j)。
常见核函数:
-
线性核: K(x_i,x_j) = x_i\cdot x_j
-
多项式核: K(x_i,x_j) = (x_i\cdot x_j + 1)^d
-
RBF 核(高斯核): K(x_i,x_j) = \exp(-\gamma |x_i-x_j|2)
六、SVM 的优点与缺点
七、SVM 的直观流程
-
数据准备(数值化、标准化)
-
选择核函数(线性/多项式/RBF等)
-
训练模型(求解最优 w, b)
-
确定支持向量
-
对新数据 x_{\text{new}},计算
想象你要在操场上画一条线,把两堆石头分成左右两边。
你不仅要分开,还要尽量离两堆石头都远一点。
离线最近的那几颗石头,就是支持向量。
如果石头分得很乱(非线性),那就换个“维度”看,比如从地上看不分得开,但从天上俯视就能画出一条线。

