机器学习入门 9：人工神经网络 (Artifical Neural Networks)

一、核心思想

人工神经网络的基本理念是：

复杂的非线性函数可以通过简单计算单元（节点）的组合来学习得到。

就像人脑由大量神经元（neurons）组成，每个神经元接收输入信号、做简单运算、然后输出信号。ANN 模拟这种结构：

节点（nodes） ⇢ 神经元
有向边（edges） ⇢ 神经元之间的连接
边的权重（weights） ⇢ 连接强度

最简单的模型叫 感知机（Perceptron） 。

截屏2025-10-30 09.39.29

二、感知机（Perceptron）

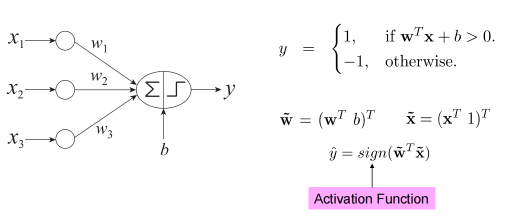
感知机是一个线性分类器，类似逻辑回归（只是激活函数不同）。

(1) 架构

每个输入特征 x_1,x_2,...,x_d 对应一个权重 w_1,w_2,...,w_d，还有一个偏置 w_0。

模型计算：

y=sign(w_0+w_1x_1+w_2x_2+...+w_dx_d)y=sign(w_0+w_1x_1+w_2x_2+...+w_dx_d)

如果结果为正，则预测一类；为负，则预测另一类。

(2) 学习规则

不断调整权重，使预测输出 $\hat{y}$接近真实标签 $y$。

更新公式为：

w_j←w_j+\lambda(y−\hat{y})x_jw_j←w_j+\lambda(y−\hat{y})x_j

其中：

\lambda：学习率（learning rate）
若预测正确，则不更新；若预测错，则调整权重方向。

每次遍历所有样本叫一个 epoch。

三、感知机的局限

感知机只能学习线性可分的边界。

比如：

x1	x2	y
0	0	-1
1	0	1
0	1	1
1	1	-1

这是著名的 XOR（异或）问题。任何一条直线都不能把正负样本完全分开。→ 感知机算法无法收敛。

机器学习入门补1: 收敛¹

四、多层神经网络（Multi-layer Neural Network）

为解决非线性问题，我们引入隐藏层（Hidden Layers） 。

每个隐藏层的节点接收上一层的输出，并将激活值传给下一层。整个结构叫 前馈神经网络（Feedforward Neural Network） 。

🧠 隐藏层的作用：

将输入空间非线性变换为新的特征空间；
逐层提取更抽象的特征；
具有足够的层数（深度）后，可以逼近任何复杂函数。

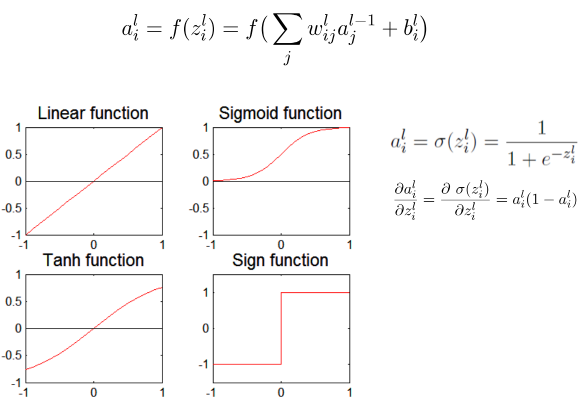
五、激活函数（Activation Function）

用于给模型增加非线性。

常见类型：

函数	表达式	特点
Sigmoid	σ(x)=1/(1+e−x)	输出在(0,1)，平滑但易梯度消失
Tanh	tanh⁡(x)	输出(-1,1)，中心对称
ReLU	f(x)=max⁡(0,x)	收敛快，不易梯度消失
Leaky ReLU	f(x)=max⁡(0.01x,x)	避免死ReLU问题

六、反向传播算法（Backpropagation, BP）

是多层网络的学习核心。

正向传播：计算预测值 \hat{y}
计算误差：用损失函数 L(y,\hat{y})

那么反向传播我们要让模型的预测值 $\hat{y}k$ 尽可能接近真实值 $yk$。

于是定义一个损失函数（Loss Function）来衡量误差，比如：

E(w,b)=\sum_{k=1}^1(yk−\hat{y}k)^2

也叫 均方误差 (Squared Loss) 。

“梯度下降”就是沿着损失函数下降最快的方向去更新参数。换句话说，让误差变小的方向走一点点。

更新规则：

wij←wij−λ\frac{∂L}{∂w_{ij}^{(l)}}

b_i^{(l)}\larr b_i^{(l)}-\lambda\frac{∂E}{∂b_i^{(l)}}

其中：

\lambda：学习率（步子大小）
\frac{∂E}{∂w_{ij}}：梯度（权重对误差的敏感度）

SGD（随机梯度下降）

与其一次用全部数据，不如每次只用一小部分数据更新，速度更快：

SGD：一条样本更新一次；
Mini-batch SGD：一小批样本更新一次。

Computing Gradients（如何求梯度）

上面说的 \frac{∂E}{∂w_{ij}}，怎么求？

1. 链式法则（Chain Rule）

每个神经元的输出是：

a_i^{(l)}=f(z_i^{(l)})=f(∑_jw_{ij}^{(l)}a_j^{(l−1)}+b_i^{(l)})

所以梯度分解为三部分：

\frac{∂Loss}{∂w_{ij}^{(l)}}=\frac{∂Loss}{∂a_i^{(l)}}×\frac{∂a_i^{(l)}}{∂z_i^{(l)}}×\frac{∂z_i^{(l)}}{∂w_{ij}^{(l)}}

2. 以 Sigmoid 激活函数为例

f(z)=\frac{1}{1+e^{−z}}⇒f′(z)=a_i^{(l)}(1−a_i^{(l)})

于是：

\frac{∂Loss}{∂w_{ij}^{(l)}}=δ_i^{(l)}×a_i^{(l)}(1−a_i^{(l)})×a_j^{(l−1)}

这里的 $δ_i^{(l)}$就是“误差信号”，表示第 i 个神经元对总误差的影响。

那每一层的 $δ_i^{(l)}$ 怎么算？

反向传播就是计算每层 δ 的方法。

1. 输出层（Output Layer）

对于最后一层（输出层）：

δ^L=\frac{∂Loss}{∂a^L}=2(a^L−y)

(来自平方误差对输出的导数）

2. 隐藏层（Hidden Layer）

通过链式法则，误差往前“传”：

δ_j^{(l)}=∑_iδ_i{(l+1)}×a_i^{(l+1)}(1−a_i^{(l+1)})×w_{ij}^{(l+1)}

意思是：

每个隐藏层的误差是由它对下一层误差的贡献决定的；
所以要从输出层往输入层逐层计算；

3. 训练过程总结

前向传播（Forward Pass）
输入 → 隐藏层 → 输出层，计算预测值；
计算损失（Compute Loss） ；
反向传播（Backward Pass）
从输出层往前计算每层的梯度；
梯度下降更新参数；
重复多轮（Epoch）直到误差收敛。

总结成一句话：

前向传播算输出，反向传播算梯度，梯度下降去更新。

整个过程就像：

往前试一遍，看错多少；
往回传递误差信息；
调整每条连接的“力度”；
重复到模型学会为止。

七、网络设计与训练细节

1️⃣ 输入层节点数（Input layer）

每个数值型或二元变量对应一个节点；
每个类别变量（categorical）如果有 k 种取值，需要用 k 个节点（One-hot 编码）或 l$og⁡_2k$ 个节点（编码方式）。

例子：
性别（男/女） → 1 个节点
颜色（红、绿、蓝） → 3 个节点（one-hot）

2️⃣ 输出层节点数（Output layer）

二分类问题（比如猫狗识别）：1 个节点；
多分类问题（比如10种数字）：k 或 $log_2k$个节点。

3️⃣ 隐藏层数量与节点数（Hidden layers）

层数越多，模型越复杂；
每层节点越多，模型的表达能力越强，但也更容易过拟合；
一般经验：从小网络开始，逐步加深。

4️⃣ 权重初始化与偏置（Initial weights & biases）

一般随机初始化（比如 Xavier、He 初始化）；
不可全设为 0，否则所有节点学到相同东西。

5️⃣ 训练参数（Training parameters）

包括：

学习率（learning rate）
训练轮数（epochs）
mini-batch 大小（mini-batch size）
优化器（SGD, Adam, RMSProp 等）

这些参数决定了模型学习的速度和稳定性。

八、Characteristics of ANN（ANN 的特点）

✅ 优点

通用逼近器 (Universal Approximator)
多层神经网络理论上可以逼近任何连续函数。
（这就是“深度学习能学任何复杂模式”的理论基础。）
自动学习特征
不用人工提取特征，模型会自己学哪些特征最有用。
能处理多余或无关特征
因为权重会自然减弱不重要的输入。

⚠️ 缺点

容易过拟合（Overfitting）
网络太大时，会把训练集“记住”，泛化能力下降。
梯度下降可能陷入局部最小值（Local Minimum）
因为误差函数不一定是凸的。
训练慢但预测快
训练时计算量大，但预测时只需前向传播。
对噪声敏感
噪声数据会导致误差传播，影响权重更新。
难以处理缺失值（Missing attributes）
神经网络要求输入完整。

九、对比

模型	能否处理非线性	学习机制	优点	缺点
感知机	否	单层线性	简单、快速	无法处理复杂问题
多层感知机 (MLP)	是	反向传播	可逼近任意函数	训练慢、易过拟合
深层网络 (Deep ANN)	是	BP + 优化技巧	强大特征学习能力	需大量数据与计算资源

十、拓展

1️⃣ 关键基础：计算能力 & 数据

现代 GPU 让多层网络的训练成为可能；
大规模标注数据集（如 ImageNet）提供了足够的样本；
批量训练（mini-batch SGD）和自动微分库（PyTorch, TensorFlow）简化了训练。

2️⃣ 算法层面的改进

ReLU 激活函数：让深层网络训练更稳定；
正则化技巧：Dropout、L2、BatchNorm 等防止过拟合；
预训练 (Pre-training) ：
- 有监督的（在大数据上先训练，再迁移）；
- 无监督的（用自编码器 auto-encoder 学表示）。

3️⃣ 特化网络结构

架构	典型任务
CNN（卷积神经网络）	图像
RNN（循环神经网络）	序列、文本、时间序列
ResNet（残差网络）	很深的网络（上百层）也能稳定训练

4️⃣ 生成模型（Generative Models）

GAN（Generative Adversarial Networks）
通过“生成器 vs 判别器”的博弈生成真实感数据（图像、语音、艺术等）。

分享

机器学习入门 9： 人工神经网络 (Artifical Neural Networks)