机器学习入门 补1: 收敛

一、什么叫“收敛”

在机器学习里，“收敛（convergence）”指的是：

当算法经过若干次迭代后，模型的参数（权重）不再发生显著变化，也就是说，它已经学到了一个​稳定的、合适的解。

对感知机来说，这个“稳定的解”就是：
一组权重 w_1,w_2,...,w_d和偏置 w_0，能把训练样本完美分类。

如果能找到这样的一组参数，我们说感知机算法​收敛​；
如果找不到（即权重一直在变、误分类点反复出现），那就叫​无法收敛。

二、为什么会“无法收敛”

感知机是一个​线性模型，它的决策边界是一条直线（二维）、或超平面（高维）。

所以它​只能学习线性可分的数据集：

• ✅ 线性可分：能画出一条直线，把两类点完全分开；

• ❌ 非线性可分：不论怎么画直线，总有一部分点被错分。

举个例子👇：

✅ 线性可分的情况

这些点能被一条直线完美分开，所以感知机算法会在有限步内找到那条线，权重趋于稳定 → ​收敛。

❌ 非线性可分的情况：XOR 异或问题

不论你怎么画直线，总会有至少一个点被错分。
于是感知机算法就会在不断修正权重、却永远无法使所有样本都正确分类。→ 它会在参数空间中“打转” ，也就是：

错误一会儿变少、一会儿又变多，永远找不到一个完美的决策边界。

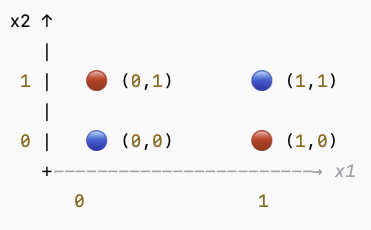
你可以试着画任意一条直线，想把所有红点（+1）和蓝点（-1）分开 —— 不可能做到。

• 无论怎么画，总会有一个红点和一个蓝点在同一边；

• 因为它们是“对角分布”的；

• 所以感知机（只会画直线）永远无法找到完全正确的分类面；

• 因此它在训练时会：

  • 一会儿修正左下角的错误；

  • 一会儿又把右上角的点错分；

  • 来回震荡，永远不收敛。

感知机的本质是一条“直线划分”：

w_1x_1+w_2x_2+b=0但 XOR 需要一条“弯曲的边界”，像这样：

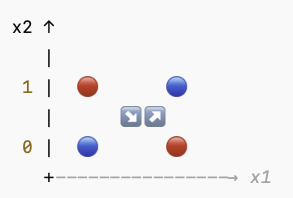
只有加入 非线性（例如通过隐藏层或特征变换）才能做到。

三、数学上的说明

感知机的收敛定理（Perceptron Convergence Theorem）指出：

如果数据集是线性可分的，感知机算法一定会在有限步内收敛。

反之，如果数据​不可线性分割：

• 算法在更新时不会停止；

• 权重会不断震荡；

• 训练误差不会降到 0。

四、通俗比喻

想象你在调一条直线去“刚好分开”红点和蓝点。

• 如果红蓝两边确实能被一条直线分开，你调几次总能找到那条线（收敛）；

• 如果红蓝混在一起，不论你怎么调，这条线总会“压到”某些红点或蓝点（无法收敛）。

五、解决办法

当发现“无法收敛”时，通常可以：

1. 增加特征维度（例如加上 x_1×x_2，使问题线性可分）；

2. ​使用多层神经网络（隐藏层可自动学习非线性特征）；

3. ​改用支持向量机 (SVM) 或决策树等非线性模型。